Announcements
Latest News
October 2024
- TC integration efforts by the NRC-HAA team commenced.
May 2024
- The new GPI 2.0 pyramid wavefront sensor was installed on the GPI 2.0 AO bench
June 2023
- Old adaptive optic was removed by UCSD team at UND facilities.
May 2022
- GPI 1.0 has been shipped on May 6th to the University of Notre Dame in Indiana, where the upgrades will be taking place.
August 2020
- GPI 1.0 is decommissioned at Gemini South, after being in nearly continuous operation since 2013.
What is GPI 2.0?
 Gemini Planet Imager 2.0 (GPI 2.0) is an upgrade of the GPI instrument previously located at Gemini South. The upgrade includes an enhanced high-sensitivity wavefront sensor, newcoronagraph masks with smaller inner working angles or higher throughput, new spectrographic modes, and software/operability improvements. GPI 2.0 is an extreme adaptive-optics imaging polarimeter and integral-field spectrometer, which will provide diffraction-limited data between 0.97 and 2.4 microns with a Strehl Ratio in H-band of ~0.9 down to 12th magnitude stars and will continue to operate, albeit with a decreased performance, beyond the 14th magnitude. The system should provide contrast ratios of 107 for companions at separations of 0.2-1.0" in a 1-2 hour observation thanks to an upgrade of its coronagraph. The science instrument will also be upgraded to provide a single-shot YJHK spectroscopy at R~12 and higher spectral resolution in single bands (R~40 in H-band). The control software will be updated to significantly increase the efficiency and robustness of GPI operations. The dual-beam polarimetry will remain unchanged. GPI 2.0 will still be capable of detecting point sources down to H=20, with ≥5σ, in 1 hour in absence of photon noise from a bright companion.
Gemini Planet Imager 2.0 (GPI 2.0) is an upgrade of the GPI instrument previously located at Gemini South. The upgrade includes an enhanced high-sensitivity wavefront sensor, newcoronagraph masks with smaller inner working angles or higher throughput, new spectrographic modes, and software/operability improvements. GPI 2.0 is an extreme adaptive-optics imaging polarimeter and integral-field spectrometer, which will provide diffraction-limited data between 0.97 and 2.4 microns with a Strehl Ratio in H-band of ~0.9 down to 12th magnitude stars and will continue to operate, albeit with a decreased performance, beyond the 14th magnitude. The system should provide contrast ratios of 107 for companions at separations of 0.2-1.0" in a 1-2 hour observation thanks to an upgrade of its coronagraph. The science instrument will also be upgraded to provide a single-shot YJHK spectroscopy at R~12 and higher spectral resolution in single bands (R~40 in H-band). The control software will be updated to significantly increase the efficiency and robustness of GPI operations. The dual-beam polarimetry will remain unchanged. GPI 2.0 will still be capable of detecting point sources down to H=20, with ≥5σ, in 1 hour in absence of photon noise from a bright companion.
Science Cases
- lower mass planets around younger stars
- higher mass planets around older stars
- closer (4-10 AU) orbits
- characterization of the distribution peak of giant planets around solar-type stars
- differentiate between cold-start (core accretion) and hot-start (disk collapse) formation models
- very young stars and transitional disks
- planet variability and abundances
- AGN jets, both spectroscopic and polarimetric
- asteroids and other solar system bodies
Main Upgrades
- EMCCD-based pyramid wavefront sensor
- broadband low spectral resolution prisms
- redesigned apodized pupil Lyot coronagraph (APLC)
- new instrument calibration unit with a new-generation self-coherent camera
Capabilities
All capabilities listed below are the goals of the upgrade and are subject to change.
- AO operable 0-14th mag, with a graceful degradation after 13th mag
- Strehl ratio 0.9 for stars brighter than H=12
- contrast ratio 107 at separations 0.2-1.0"
- wavelength range 0.97-2.4µm
- plane options
- coronagraphy (APLC)
- direct (no APLC)
- non-redundant mask (NRM)
- IFU spectroscopy
- single-shot YJHK at R~12
- single-band at R~40
- 2.7" square field of view
- 0.014" per lenslet spatial sampling
- polarimetry
- dual-channel polarimetry
- Y, J, H and K bands
Timeline
Commissioning is expected to begin towards the end of 2025 with the aim to offer it to the community in 2026.
Instrument Design
GPI 2.0 is an extreme adaptive optics system. Figure below highlights the main instrument design changes between the original GPI 1.0 system and GPI 2.0.
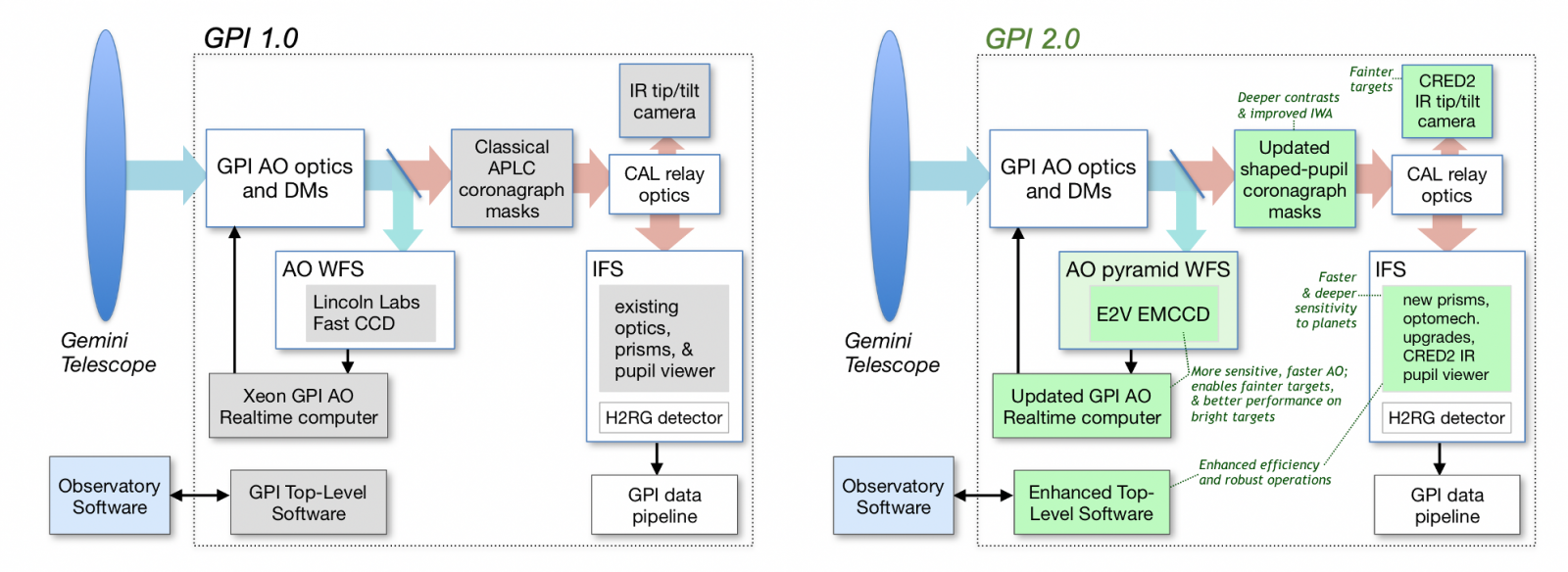
Figure 1: Schematic of the GPI 1.0 subsystems (left) and GPI 2.0 (right). Components being upgraded are highlighted in green.
(Credit: Chilcote et al., 2020, SPIE 11447, 114471S.)
GPI 2.0 Team
- Jeffrey Chilcote, University of Notre Dame, Project Leader
- Quinn Konopacky, UC San Diego
- Bruce Macintosh, UC Observatories
- Dmitry Savransky, Cornell University
- Oyku Galvan, Gemini, Project Manager
- Teo Mocnik, Gemini, Instrument Scientist
- Garima Singh, Gemini, AO Scientist
- Christy Cunningham, Gemini, Systems Engineer
- Carlos Quiroz, Gemini, Software Engineer